Romps, Accurate expressions for the dew point and frost point derived from the Rankine-Kirchhoff approximations, JAS, 2021

Code

R: dewpoint.R test.R

Python: dewpoint.py test.py

Matlab: dewpoint.m test.m

Fortran 90: dewpoint.f90 test.f90 f90_makefile

Errata

On the last line of page 2114, R_v should be R_vT_trip. This has been corrected in the PDF below. Thank you to David Sproles for catching this typo.

Paper

PDF

BibTeX

DOI

Description

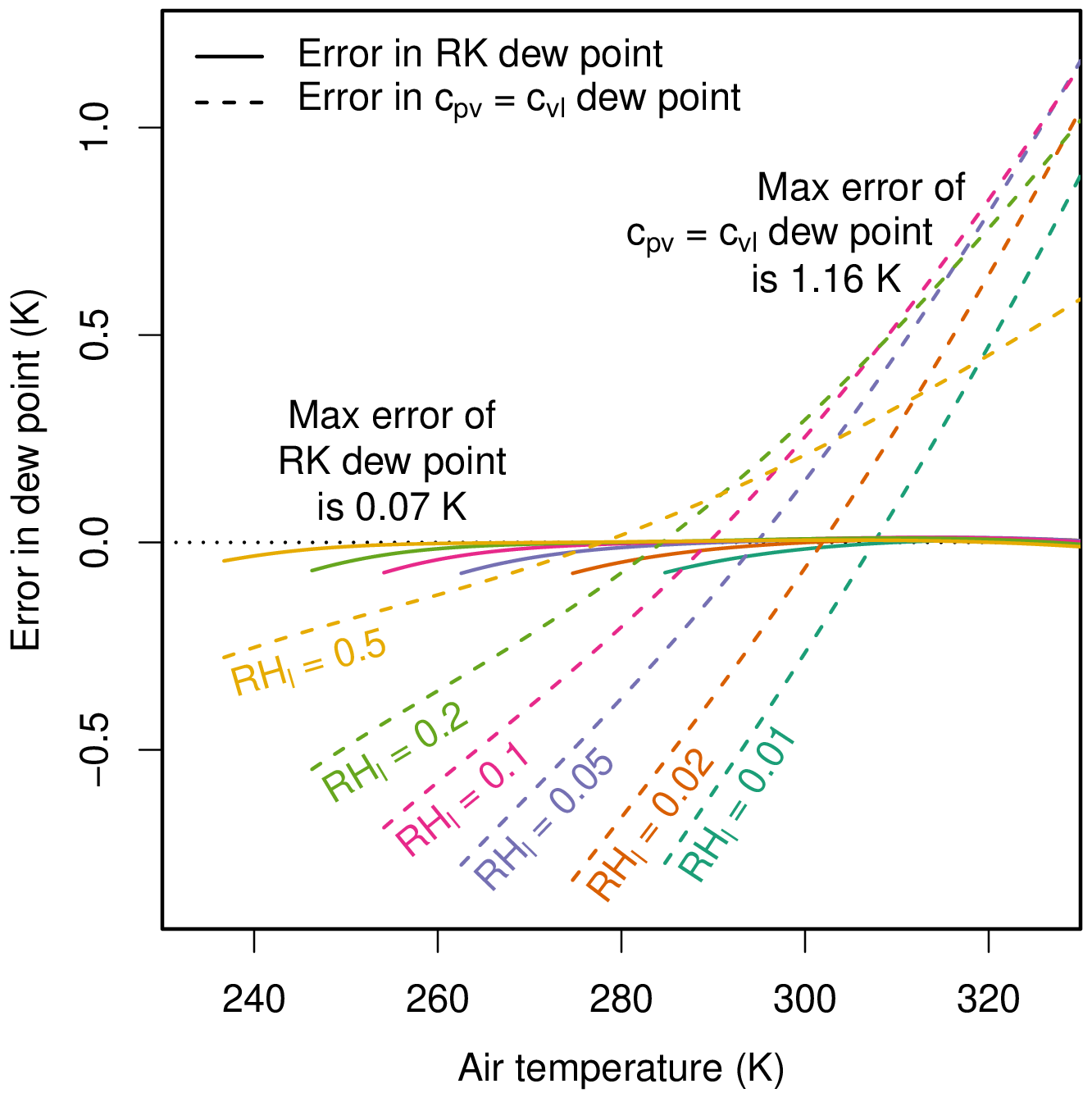
The dew point is the temperature to which air must be cooled at constant pressure for dew to form (or, more precisely, to reach saturation with respect to a plane of liquid water). It is a function of the air temperature and relative humidity, and it is usually calculated using a root solver that searches iteratively for the temperature that exactly produces saturation. While there is an explicit and analytic expression for the dew point in the literature, it produces errors as large as a Kelvin.

The Rankine-Kirchhoff approximations provide a self-consistent set of equations with which to describe the thermodynamics of moist air to a high degree of accuracy. The underlying approximations are that dry air and water vapor are ideal gases, that heat capacities are constant, and that condensates have zero specific volume. These approximations were used in an earlier paper on the lifting condensation level (LCL) to produce an expression for the lifting condensation level (LCL) that was explicit, analytic, and exact in the sense of having errors less than the empirical uncertainty.

In this short note, the Rankine-Kirchhoff approximations are used to generate explicit, analytic, and accurate expressions for the dew point and frost point. As shown in the figure below, the existing analytic expression has errors as large as 1 K whereas the new dew-point expression is accurate to better than 0.07 K, which is comparable in magnitude to the uncertainties of laboratory measurements.