Romps, Seeley, and Edman, Why the forcing from carbon dioxide scales as the logarithm of its concentration, J Climate, 2022
Short summary
Long summary
Paper
Description
It is well-known that the radiative forcing (i.e., effected decrease in outgoing longwave radiation) from carbon dioxide is approximately logarithmic in its concentration, producing about four watts per square meter of global-mean forcing for each doubling. These are basic facts of climate science that serve as a foundation of our understanding of anthropogenic global warming. Yet competing explanations for these basic facts have been given in the literature in recent years.
Here, the various pieces of physics that conspire to generate the logarithmic forcing are explored in detail using both line-by-line radiative-transfer calculations and a simple pencil-and-paper model for the forcing. An essential part of the mechanism is the particular distribution of absorption coefficients within the 15-micron band of carbon dioxide. An alternative explanation that has been given repeatedly in the literature, which does not depend on the spectrum of carbon dioxide but hinges on the tropospheric lapse rate instead, is shown to be neither necessary nor sufficient to explain the logarithmic forcing of carbon dioxide and to be generally inapplicable to well-mixed greenhouse gases in Earth’s atmosphere.
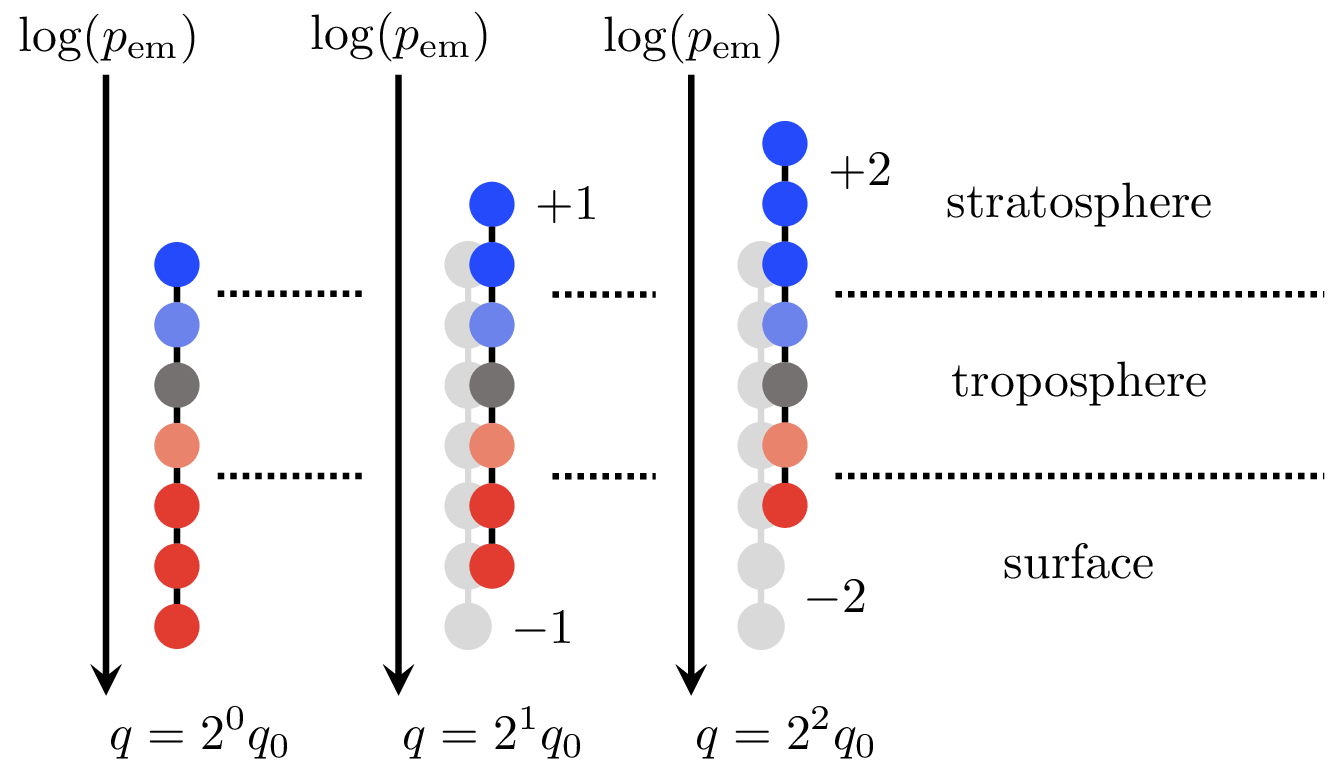
In an atmosphere with no greenhouse gases, all wavenumbers would emit to space from the surface. Once a greenhouse gas is introduced, some wavenumbers emit to space from the vicinity of a colder emission pressure pem in the atmosphere, thereby reducing the outgoing longwave radiation. Due to the particulars of the absorption spectrum of carbon dioxide, the wavenumbers affected by carbon dioxide are distributed uniformly throughout an interval of log(pem) with the wavenumbers with the highest κ emitting to space from the stratosphere and the wavenumbers with the lowest κ emitting from the Earth's surface. Every time the CO2 concentration is doubled, the entire interval of log(pem) moves to lower values by log(2)/2. This effectively moves some emission to space from the warm surface to the cold stratosphere. For every successive doubling, the log(pem) interval moves lower by log(2)/2, thereby effectively moving the same-sized set of wavenumbers from the surface to the stratosphere. The size of this set is easily calculated from the spectrum of CO2, as measured in the laboratory, allowing for a pencil-and-paper calculation of the radiative forcing.