Romps and Kuang, A transilient matrix for moist convection, JAS, 2011
Paper
Description
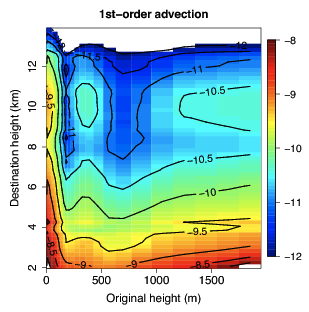
A transilient matrix quantifies the nonlocal transport of fluid by eddies: for every height z, it gives the distribution of starting heights z' for the eddies that arrive at z. The rows of the matrix correspond to the initial heights of eddies, and the columns correspond to the final heights. For example, the element bij gives the rate of mass eddying from zj to zi. If this matrix can be diagnosed for a fluid flow, then it provides valuable information about the behavior of eddies.
In this paper, a transilient matrix is defined that does not suffer from the problem of convective structure memory that has plagued previous approaches. The method of diagnosing this matrix involves the use of passive tracers that are injected at different heights and allowed to decay radioactively. In a cloud-resolving simulation of deep convection, the transilient matrix shows that two thirds of the subcloud air convecting into the free troposphere originates from within 100 meters of the surface. This finding clarifies which initial height to use when calculating convective available potential energy from soundings of the tropical troposphere.
Log-10 of the elements of the transilient matrix for deep convection. This shows that the boundary-layer parcels detraining in the troposphere (between 2 and 14 km on the y axis) come primarily from the first 100 meters of the boundary layer (0 to 100 meters on the x axis).