Romps, The dry-entropy of a moist atmosphere, JAS, 2008
Paper
Description
One of the big unresolved questions in tropical atmospheric dynamics is what sets the buoyancy scale of deep convection: why do updrafts have a typical temperature excess of 1 K? Why not 0.1 K or 10 K? In the case of dry convection, the buoyancy of plumes is set by the need for sensible heat fluxes to balance the radiative cooling. Another way to get this answer is to use the entropy budget: the diabatic sources of entropy, Q/T, set the dissipation, which, in turn, sets the buoyancy of plumes. This is the natural "heat engine" picture of dry convection, with heating and cooling at different temperatures leading to work performed by the piston-like plumes.
In moist convection, the fluxes of sensible heat play only a small role in balancing the radiative cooling. And, the entropy budget is complicated by the presence of many additional terms related to water vapor. This paper distinguishes between dry entropy (cp log theta) and the more complicated moist entropy. It is argued that the dry entropy leads to a more intuitive description of the atmosphere as a heat engine: heat is added by condensation at warmer temperatures than radiative cooling, which generates the sensible heat fluxes that set the buoyancy. This dry-entropy budget is derived for an atmosphere with fusion and realistic heat capacities and is studied in DAM, a cloud-resolving model built specifically to close this budget.
The dry-entropy budget for radiative-convective equilibrium.
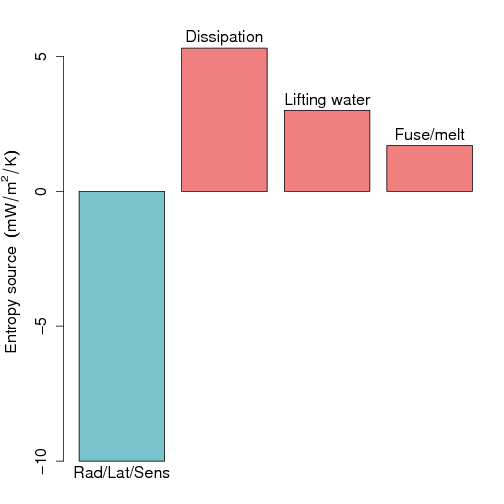
It is shown, both from theory and from simulations, that the dry-entropy budget may be described as a balance between six terms. The first three terms are generated by the addition and removal of sensible heat by surface heating, condensation in the free troposphere, and radiative cooling of the atmosphere. Together these three terms make a net entropy sink that is balanced by three entropy sources. In order of decreasing magnitude, these entropy sources are generated by dissipation (as generated by the bouyancy of plumes), the lifting of water (the "elevator"), and the freeze-melt cycle of condensates near the melting line (an effective "conductor" of heat from the relatively warm melting line to the relatively cold troposphere above it).