Romps and Vogelmann, Methods for estimating 2D cloud size distributions from 1D observations, JAS, 2017
Paper
Description
An airplane, on a linear flight path, will sample cloud chord lengths Li, with i ranging from 1 to the total number of clouds sampled. How do we convert from that set of Li to the actual distribution of cloud sizes?
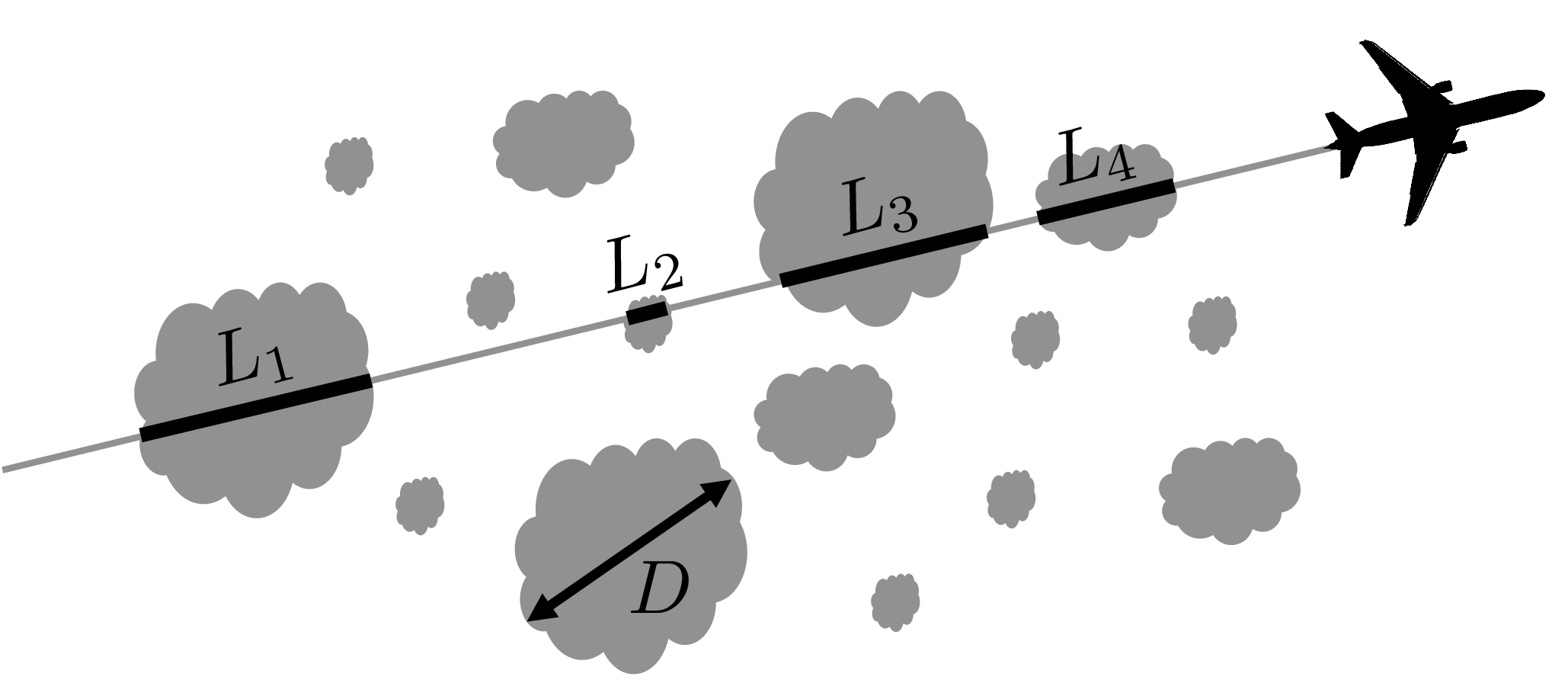
For a given patch of sky, the distribution of horizontal cloud sizes plays an important role in setting the total cloud cover, the cloud radiative forcing, convective entrainment rates, and the likelihood of precipitation. Despite the importance of the cloud-size distribution, it is not often measured directly. Instead, during field campaigns and at meteorological stations, cloud sizes are usually inferred indirectly from linear sampling by aircraft, radar, lidar, or radiometer. Unfortunately, the distribution of cloud-chord lengths measured in this way is not the same as the distribution of cloud sizes. This mismatch is caused by two effects: 1. an off-center sampling of a cloud will tend to yield a chord that is smaller than the true diameter, biasing the distribution to smaller sizes, and 2. large clouds are more likely to be sampled than small clouds, biasing the distribution to larger sizes.
Here, a simple method is proposed for calculating the area-weighted mean cloud size and for approximating the 2D size distribution from the 1D cloud chord lengths measured by aircraft and vertically pointing lidar and radar. This simple method (which is exact for square clouds) compares favorably against the inverse Abel transform (which is exact for circular clouds) in the context of theoretical size distributions. Both methods also perform well when used to predict the size distribution of real clouds from a Landsat scene. As a demonstration, the methods are applied to aircraft measurements of shallow cumuli during the RACORO campaign, which then allow for an estimate of the true area-weighted mean cloud size.